TeXify: Typesetting for the Web

Abstract

This page introduces TeXify, a library for performing high-quality typesetting within web browsers. It is designed to require only basic familiarity with Hyper-Text Markup Language (HTML) from the author — no knowledge about JavaScript or Cascading Style Sheets (CSS) is necessary. Although not as sophisticated as the TeX typesetting engine, the output produced is of much higher quality than that which can be obtained by unstyled HTML.

Introduction

The TeX typesetting system was released by Donald Knuth in the late 1970s, as one of the first programs for producing high-quality digital typography. In the following decade, Tim Berners-Lee initiated the World Wide Web project, releasing it to the public in the early 1990s.

Over thirty years after its release, TeX remains the state-of-the-art for professionally publishing technical articles, whilst being accessible enough to be used directly by authors. On the other hand, although the Web became a phenomenal success for distributing and linking documents over the Internet, typographical quality was sorely lacking (see Figure 1) — a problem which remained unresolved for a number of decades after its introduction.

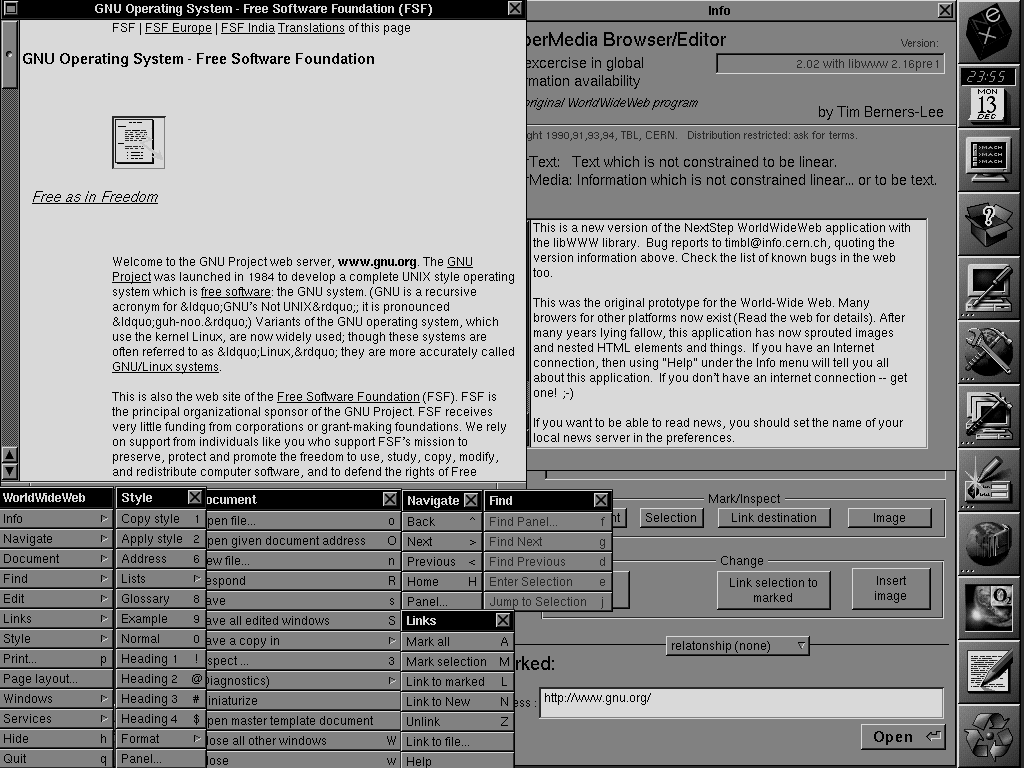
The Web's poor typographical support lead to the popularity of the Portable Document Format (PDF) for publishing techical articles, even in cases where fixed-format documents were not strictly required. Indeed, fixed-format PDF documents have become burdensome for the same reason the Web has been successful — flowing hyperlinked text is much easier for readers to consume across a variety of devices.

Fortunately, this situation has improved markedly in recent years, particularly with the introduction of CSS level 3. This has allowed web designers to compensate for the poor level of typography provided in web browsers by default. The aim of the TeXify project is to combine all of these individual libraries in such a way that authors merely need to include a single extra line in their HTML documents in order to take advantage of modern web typography.

Usage

Bookmarklet

Simply click-and-drag the following link to your bookmarks bar:
TeXify
When visiting any webpage, re-style it by clicking the “TeXify” button in your bookmarks bar.

Embedding

TeXify is still experimental and not yet ready for public use. Please visit the GitHub project for more information.

Examples

A New Limit on Time-Reversal Violation in Beta Decay
The Applications of Probability to Cryptography by Alan Turing
arXMLiv — click any of the preview links
The Elements of Typographic Style Applied to the Web

Lorem Ipsum

Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.

Emphatic

Strong

Strong and Emphatic

Equations

The Lorenz Equations

\[\begin{aligned} \dot{x} & = \sigma(y-x) \\ \dot{y} & = \rho x - y - xz \\ \dot{z} & = -\beta z + xy \end{aligned}\]

The Cauchy-Schwarz Inequality

\[ \left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right) \]

A Cross Product Formula

\[ \mathbf{V}_1 \times \mathbf{V}_2 = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial X}{\partial u} & \frac{\partial Y}{\partial u} & 0 \\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v} & 0 \end{vmatrix}\]

The Binomial Distribution

The probability of getting \(k\) heads when flipping \(n\) coins is: \[ P(E) = {n \choose k} p^k (1-p)^{ n-k} \]

An Identity of Ramanujan

\[ \frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}}{1+\frac{e^{-4\pi}}{1+\frac{e^{-6\pi}}{1+\frac{e^{-8\pi}}{1+\ldots}}}} \]

A Rogers-Ramanujan Identity

\[ 1+\frac{q^2}{1-q}+\frac{q^6}{(1-q)(1-q^2)}+\cdots = \prod_{j=0}^{\infty}\frac{1}{(1-q^{5j+2})(1-q^{5j+3})}, \quad\text{for }|q|<1. \]

Maxwell's Equations

\[\begin{aligned} \nabla \times \vec{\mathbf{B}} - \frac1c\,\frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\ \nabla \times \vec{\mathbf{E}} + \frac1c\,\frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\ \nabla \cdot \vec{\mathbf{B}} & = 0 \end{aligned}\]